Hyperbolic Paraboloid

A hyperbolic paraboloid is a type of quadric surfaces. If it is centered at the origin, then its equation could be one of the equations below:

 


Hyperbolic paraboloid has a very interesting shape. It is a combination of hyperbola and parabola. For example, if we look at the graph of the equation below (the first type of equations above), 

and

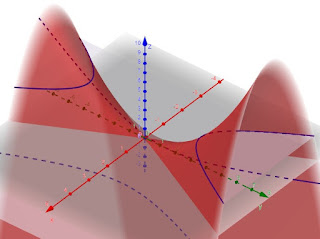
1. 'slice' the surface horizontally using planes , we get hyperbola shapes (the leftmost graph below). Take note at z = 0, we get a cross, 'x'. z = 0 serves as a threshold whether the direction of hyperbola opening changes its direction.
2. 'slice' the surface vertically using planes , we get parabola shapes (the middle graph below);
3. 'slice' the surface vertically using plane x = 0, we get a parabola (the rightmost graph below). Even if you 'slice' the surface vertically with , you will still get parabolas. To avoid the graph looks too 'crowded', I only use one plane to 'slice' the surface.

Hyperbolic paraboloid is also called as saddle due to its shape. Referrng to this example, imagine that there is an invisible horse facing the y-axis direction with its saddle on it, with the sitting place facing up (z > 0). 

You may change the values of a, b and c to see the changes of the graph. Type 1 is the first equation stated on top of this article, Type 2 is the second and Type 3 refers to the third equation. Please un-tick all choices before you change to another type of equation. You may click here if you want to have better viewing experience.

If the surface is shifted to be centered at (h, k, l), then the equations above will look like the equations below:

You may refer to other quadric surfaces on the surface shifting concept. It applies the same here.

Betty, created with GeoGebra and Thomas Calculus, Pearson.