An elliptical paraboloid is a type of
quadric surfaces. It has an elliptical opening. Somehow, the opening can be circular sometimes, depending on the values of
a,
b and
c. These values will also affects the direction of the opening, either towards the positive side of the axis or the other way round. If its vertex falls on the origin, then its equation could be one of the equations below.
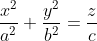
If the vextex falls at (h, k, l), then its equation could be one of the equations below:
^2}{a^2}+\frac{(y-k)^2}{b^2}=\frac{z-l}{c} "\frac{(x-h)^2}{a^2}+\frac{(y-k)^2}{b^2}=\frac{z-l}{c}")
^2}{a^2}+\frac{(z-l)^2}{c^2}=\frac{y-k}{b} "\frac{(x-h)^2}{a^2}+\frac{(z-l)^2}{c^2}=\frac{y-k}{b}")
^2}{b^2}+\frac{(z-l)^2}{c^2}=\frac{x-h}{a} "\frac{(y-k)^2}{b^2}+\frac{(z-l)^2}{c^2}=\frac{x-h}{a}")
The box below contains all the graphs mentioned above. Tick one category at a time to view the graph. You may slide the values of
a,
b,
c,
h,
k and
l to see the changes on the graph. Observe the following matters:
- What is the axis of the graph?
- What is the opening of the graph? Elliptical or circular? How do the values of a, b and c affect the opening.
- What are the intercepts?
- What's the effect of a, b and c when it's positive or negative?
If you wish to have a better view and want to rotate the graph, just click
here.
Betty, created with GeoGebra and Thomas Calculus, Pearson.
No comments:
Post a Comment