A limaçon is a snail curve. The equations
)
and
)
give to the shape of it when
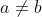
.
When
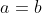
, a cardioid is formed. Try to change the values of
a and
b by dragging it. You may also drag the value of
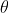
to see the forming of the curve.
Betty, Created with GeoGebra
No comments:
Post a Comment