A hyperboloid of one sheet is a type of
quadric surfaces that carries one of the equations below
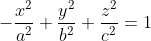
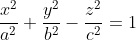
if it is centered at the origin. The position of negative sign determines the axis of the graph.
Now, if the hyperboloid of one sheet is centered at (h, k, l), the equation will look like one of the equations below:
^2}{a^2}+\frac{(y-k)^2}{b^2}+\frac{(z-l)^2}{c^2}=1 "-\frac{(x-h)^2}{a^2}+\frac{(y-k)^2}{b^2}+\frac{(z-l)^2}{c^2}=1")
^2}{a^2}-\frac{(y-k)^2}{b^2}+\frac{(z-l)^2}{c^2}=1 "\frac{(x-h)^2}{a^2}-\frac{(y-k)^2}{b^2}+\frac{(z-l)^2}{c^2}=1")
^2}{a^2}+\frac{(y-k)^2}{b^2}-\frac{(z-l)^2}{c^2}=1 "\frac{(x-h)^2}{a^2}+\frac{(y-k)^2}{b^2}-\frac{(z-l)^2}{c^2}=1")
Try to play around with the graph below and answer the questions below:
- What is the axis of the surface?
- What is the shape of the opening? Is it elliptical or circular? How do the values of a, b and c play the role on the shape?
- What are the intercepts?
Take note that the center is shown when you tick on your preference. Remember to un-tick the choice when you want to view another surface. If you wish to rotate the graph, or the graph below seems to look funny, please click
here for better viewing experience.
Betty, created with GeoGebra and Thomas Calculus, Pearson.
No comments:
Post a Comment