1) n is a unit vector and therefore |n| = 1, and
2)  for
for  .
.
area = base * height
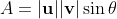
which the area is equals to the magnitude of  .
.
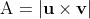
The graph below shows the parallelogram in space. The calculation at the top left of the graph is the calculation using the cross product, whereas the right uses the previous area formula. Try to move point A and B to change the shape of parallelogram and observe the area calculted using both methods.
Betty, Created with GeoGebra and Thomas Calculus, Pearson.
Now, lets take a look at a parallelogram that is formed by two vectors u and v.
The area of the parallelogram is
The area of the parallelogram is
As such we can use the cross product to find area of parallelogram formed by vectors u and v:
The graph below shows the parallelogram in space. The calculation at the top left of the graph is the calculation using the cross product, whereas the right uses the previous area formula. Try to move point A and B to change the shape of parallelogram and observe the area calculted using both methods.
Betty, Created with GeoGebra and Thomas Calculus, Pearson.

No comments:
Post a Comment