Betty, Created with GeoGebra
Welcome, my friends! This website is to help those who need help in mathematics topics especially in visualizing it. Topics covered including higher secondary to tertiary level. Interactive graphs are provided for concept exploration. Meantime, most of the topics are visualized with Geogebra. There are more to come in the future. See you around!
Monday, January 16, 2012
Spiral
A spiral is formed with a simple equation 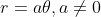 . The graph below set 'a' as positive, therefore there are two equations for you to tick. Choose whichever equation you prefer, you may choose both as well, then drag the value of 'a' according to your preference. Then, drag the value of
. The graph below set 'a' as positive, therefore there are two equations for you to tick. Choose whichever equation you prefer, you may choose both as well, then drag the value of 'a' according to your preference. Then, drag the value of  to view the forming of spiral.
to view the forming of spiral.
Saturday, January 14, 2012
Lemniscate
The equations ) and
and ) form the shape of lemniscate. If you take a look at the graph (in default setting) below, you might find out that there is no graph formed for
form the shape of lemniscate. If you take a look at the graph (in default setting) below, you might find out that there is no graph formed for 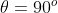 till
till 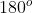 , and from
, and from  to
to 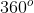 . Can you explain why? You may drag the value of 'a' to see the difference of graphs and
. Can you explain why? You may drag the value of 'a' to see the difference of graphs and  for the forming of the curve. Then, choose another equation to display its graph and compare. What can you say about these two graphs?
for the forming of the curve. Then, choose another equation to display its graph and compare. What can you say about these two graphs?
Betty, Created with GeoGebra
Betty, Created with GeoGebra
Friday, January 13, 2012
Polar
A coordinate (x,y) in xy-plane can be written in polar form ) , where r is the directed distance from (0,0) to (x, y), and
, where r is the directed distance from (0,0) to (x, y), and 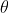 is the directed angle formed by the vector
is the directed angle formed by the vector 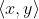 ; from the positive side of x-axis, where
; from the positive side of x-axis, where

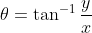
You may try to drag the value of the sliders in the graph to look at Point A and the coordinates in) and
and ) . Take note that the value of
. Take note that the value of 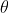 is in radian mode.
is in radian mode.
There are some interesting graphs can be obtained through polar equations, such as
Click on the links above to explore the shapes mentioned.
Betty, Created with GeoGebra
You may try to drag the value of the sliders in the graph to look at Point A and the coordinates in
There are some interesting graphs can be obtained through polar equations, such as
- Limaçon :
or
, where
- Cardioid :
or
- Rose :
or
- Lemniscate :
or
- Spiral :
Click on the links above to explore the shapes mentioned.
Betty, Created with GeoGebra
Limaçon & Cardioid
A limaçon is a snail curve. The equations ) and
and ) give to the shape of it when
give to the shape of it when 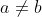 .
.
When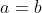 , a cardioid is formed. Try to change the values of a and b by dragging it. You may also drag the value of
, a cardioid is formed. Try to change the values of a and b by dragging it. You may also drag the value of  to see the forming of the curve.
to see the forming of the curve.
When
Betty, Created with GeoGebra
Wednesday, January 11, 2012
Sequence & Series
A sequence is a set of terms arranged in a particular order such as
while a series is the summation of the terms in a sequence, e.g.
A sequence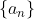 is a convergent sequence if and only if there is a finite number a where
is a convergent sequence if and only if there is a finite number a where 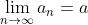 . Otherwise, the sequence is divergent. Likewise, a series
. Otherwise, the sequence is divergent. Likewise, a series 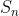 is a convergent series if and only if there is a finite number S where
is a convergent series if and only if there is a finite number S where 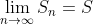 . Otherwise, the series is divergent.
. Otherwise, the series is divergent.
For example, harmonic sequence is convergent but its series is divergent. Perhaps putting the sequence and series in graph might help you to understand better. Look at the graph below, y-coordinate of point A represents the harmonic sequence while y-coordinate of point B represents summation of the harmonic series, where n is the index. Drag the value of n and observe the positions of point A & B. You'll find that point A is approaching to x-axis (y = 0) as n is getting bigger but point B keeps on rising.
Let's take a look at another type of divergent series - Geometric series with common ratio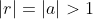 :
:
 .
.
The points in purple represent sequence and points in red represent series. Tick on the series you want to look into, and drag the values of a and/or n to observe the convergence of the sequence and series.
Now, consider 3 types of infinite convergence series:
Graph shown below is the graph of Geometric series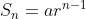 with
with 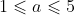 and
and  . The point in purple represents the respective sequence and the red represents the series. Look at the graph below, y-coordinate of point A represents the geometric sequence while y-coordinate of point B represents summation of the geometric series. n is the index. Drag the value of n and observe the positions of point A & B. You'll find that point A is approaching to x-axis (y = 0) as n is getting bigger but point B tends to stop rising.
. The point in purple represents the respective sequence and the red represents the series. Look at the graph below, y-coordinate of point A represents the geometric sequence while y-coordinate of point B represents summation of the geometric series. n is the index. Drag the value of n and observe the positions of point A & B. You'll find that point A is approaching to x-axis (y = 0) as n is getting bigger but point B tends to stop rising.
Try to play around with the graph below. After that, click on other choices of a and r to observe the convergence of the sequence and series given.
Betty, Created with GeoGebra
while a series is the summation of the terms in a sequence, e.g.
A sequence
For example, harmonic sequence is convergent but its series is divergent. Perhaps putting the sequence and series in graph might help you to understand better. Look at the graph below, y-coordinate of point A represents the harmonic sequence while y-coordinate of point B represents summation of the harmonic series, where n is the index. Drag the value of n and observe the positions of point A & B. You'll find that point A is approaching to x-axis (y = 0) as n is getting bigger but point B keeps on rising.
Let's take a look at another type of divergent series - Geometric series with common ratio
The points in purple represent sequence and points in red represent series. Tick on the series you want to look into, and drag the values of a and/or n to observe the convergence of the sequence and series.
Now, consider 3 types of infinite convergence series:
- Geometric series with common ratio, 0 < r < 1 :
- Geometric series with common ratio, -1 < r < 0 :
- Alternating harmonic series :
Graph shown below is the graph of Geometric series
Try to play around with the graph below. After that, click on other choices of a and r to observe the convergence of the sequence and series given.
Betty, Created with GeoGebra
Subscribe to:
Posts (Atom)