When we talks about trigonometry, we will most probably think of trigonometric functions, e.g. sine, cosine, tangent etc. Ever think of how were the graphs of these functions obtained?
Let's consider a right triangle with hypotenus (
r) of 1 unit as in the graph below (left column). If you tick the first function
 "f = sin(\theta)")
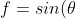at the right column, you will see the appearance of point E with the coordinate
&space;\right&space;) "\left ( \theta, f(\theta) \right )")
in the right column. Take note that
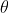
in the coordinate is shown in radian mode.
Recall the definition of the trigonometry functions as below, observe the changes of value
f (the height of point E) as you slowly drag the point C in the graph in the first column and observe the changes of the angle.
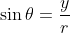
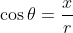
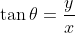
As
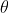
at the left column increases in the first quadrant, point E is getting higher because
y-value in (
x,
y) is getting bigger (the triangle is getting taller), resulting
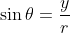
also increases; while the hypotenus,
r remains as 1.
Now, if you continue to explore other functions like
 "f = cos(\theta)")
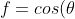and
 "f = tan(\theta)")
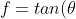, point F and point G will appear. Take note that Point E is having the coordinate of
&space;\right&space;) "\left (\theta, \sin(\theta) \right )")
, point F is
&space;\right&space;) "\left (\theta, \cos(\theta) \right )")
and point G is
&space;\right&space;) "\left (\theta, \tan(\theta) \right )")
. Observe the position of point E, F or G as you drag point C. You may choose the desire graph at the bottom right corner of the graph.
If you wish to know more about trigonometric functions, please click on the equation you are interested under Trigonometry at the right column.
Betty, Created with GeoGebra
No comments:
Post a Comment